AbudoriLab.です。今回は、SLAMと並んでロボットの自律移動のために重要な技術である経路計画についての記事になります。
本記事では、経路計画の最も基本的な手法である幅優先探索と深さ優先探索のアルゴリズムの概略を解説し、実際にプログラムを動かして両者の比較を行います。
今後も経路計画の記事をシリーズで連載していきますが、このシリーズを通して基本的な経路計画アルゴリズムのざっくりとした理解が期待できます。
経路計画アルゴリズムでは、スタック、キュー、全探索、最短経路問題、動的計画法といった競技プログラミングでお馴染みの概念がたくさん出てきますので、アルゴリズム力の底上げに繋がれば嬉しいです。
SLAMについてもいくつか紹介していますので拝読して頂けますと幸いです。
経路計画とは?
経路計画は英語ではpath planningと表記され、ロボットがある地点からある地点に移動する際の経路(パス)を計算します。
目的地に到着できる経路は数多くの候補が存在しますが、その中でも一般的な経路計画では、障害物を回避しながら最短距離の経路を計算できることが望ましいとされます。
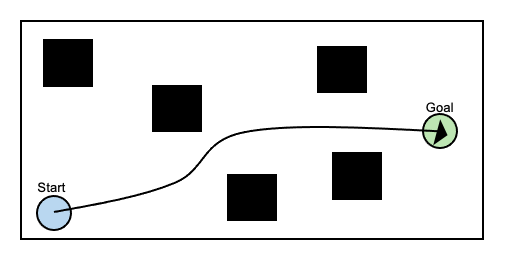
例え障害物を回避しても、下図のように大回りの経路ではロボットが大変ですね。
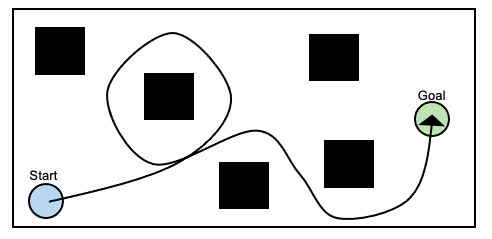
それゆえ、経路計画では、
・障害物回避
・経路長最短
の2つを満たす経路を計算することが求められます。
地図とグラフ
経路計画はグラフに対する探索アルゴリズムが基礎となります。
グラフとは、ノードとエッジという二種類の要素からなるデータ構造です。
下図はグラフの一例です。アルファベットが記載された円がノード、各ノード間の黒い線分がエッジです。エッジはノードとノードの接続を表し、エッジがないノード間は接続がありません。
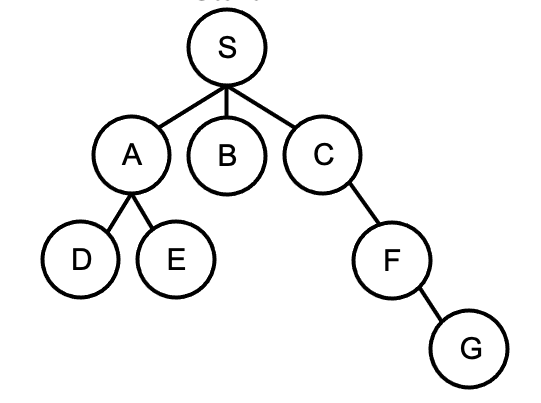
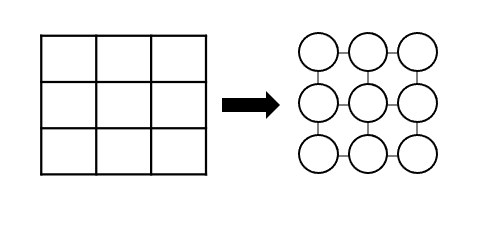
経路計画においてグラフ探索アルゴリズムを適用するには、まず地図を上記のようなグラフで表現することが必要となってきます。下図はロボットの自律移動で一般的に用いられる格子地図(グリッドマップ)を、グラフで表現した例です。ノードは地図の各グリッドです。ロボットが上下左右4方向に移動できるとすると、エッジも4方向に接続されます。
以降の章では、このようなグラフ地図に対して、アルゴリズムがどう動くかを説明していくことになります。
スポンサードリンク
幅優先探索と深さ優先探索
経路計画に適用できる、最も原始的なグラフ探索アルゴリズムが幅優先探索と深さ優先探索です。
実際には深さ優先探索は最短経路長の経路が求められないので経路計画として使われることはないのですが、基本的なアルゴリズムとして非常に有名であるため本記事では幅優先探索との比較のためにも解説します。
幅優先探索は、グラフをスタート地点から近い順にくまなく経路を探していく方法です。
ある地点に隣接する複数の次の地点を全て平等に調べ上げていくことから、「幅」優先探索と言われます。
これに対して深さ優先探索は、グラフをスタート地点から行けるところまで探索し、いけなくなったら手前まで戻って探索するアルゴリズムです。
行けるだけ「深く」探索するため「深さ」優先探索と言われます。
キューとスタック
幅優先探索と深さ優先探索のアルゴリズムを考えるとき、幅優先探索はキュー(queue)、深さ優先探索はスタック(stack)と呼ばれるデータ構造を用います。
両者はデータの保存と出し入れが出来る構造という点で共通していますが、出し入れのルールが異なります。
キューは入れた順番で最も古い要素を先に取り出します。
よって、下図のようにA, B, C, Dの順番に要素が入れられたとき、Aが最初でその後はB→C→Dの順に取り出します。
キューにおいて要素を入れる操作はエンキュー(enqueue)、取り出す操作はデキュー(dequeue)と言います。
また余談になりますが、一番古く(最初に)入った要素を最初に取り出すため、First in First Out (FIFO)とも呼ばれます。

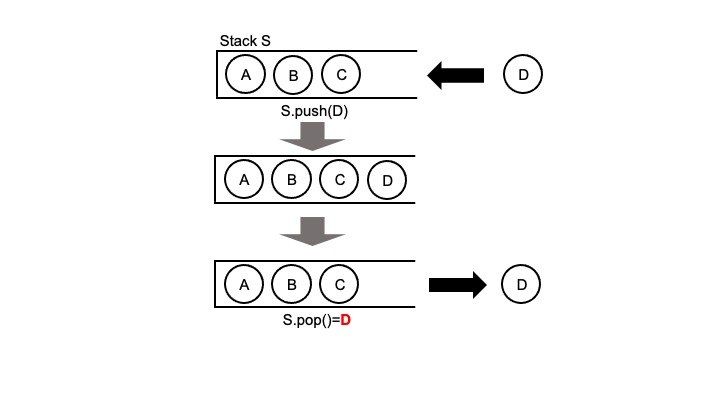
これに対してスタックは新しく入った要素の順に取り出します。
下図のようにA, B, C, Dの順番に要素が入れられたとき、Dを最初に取り出し、(その後に新しい要素が入れられなければ)C→B→Aの順に取り出されることになります。
スタックにおいては要素を入れる操作をプッシュ(push)、取り出す操作をポップ(pop)と言います。
また、一番新しく(最後に)入った要素が最初に取り出されるので、LIFO (Last in First Out)とも呼ばれます。
幅、深さ優先探索のアルゴリズム
キューとスタックのデータ構造を使って、幅優先探索と深さ優先探索がどう実現されるか動画を用いて確認します。
なお、実際の経路計画ではゴールを見つけた時点で探索は終了しますが、動画では分かりやすさのため、全地点を探索するまでアルゴリズムを動かし続けています。
初めに、幅優先探索がキューを用いて具体的にどう実行されるかをご紹介します。

キューの、FIFOの性質を利用することでスタートから近い地点(ノード)の順番に訪問済みになっていくことがわかります。
(「訪問済み」という概念を導入することで、同じ地点の二重の探索を防ぐことができます。)
続いて深さ優先探索がスタックを用いて具体的にどう実行されるかをご紹介します。

スタックの、LIFOの性質を利用することで「行けるところまで行く」という動作が実現できていることが分かります。
例えば、最初SからC, F, Gまで一直線に探索が進んでいます。
2つの探索法で面白いのは、両者で訪問済みにするタイミングが異なることです。
幅優先探索ではキューに入れるときに深さ優先探索ではスタックから取り出すときにそれぞれノードを訪問済みになるのですが、理由を考えてみると理解が深まると思います。
2つの探索手法の比較
幅優先探索と深さ優先探索を実行可能なプログラムを作成しました。
こちらを使って2つの手法の挙動をシミュレーションしてみましょう。
プログラムはpython3で記述されており、以下のリンクよりダウンロード可能です。
https://github.com/AbudoriLab-org/fundamental_path_planning/blob/main/planner.py
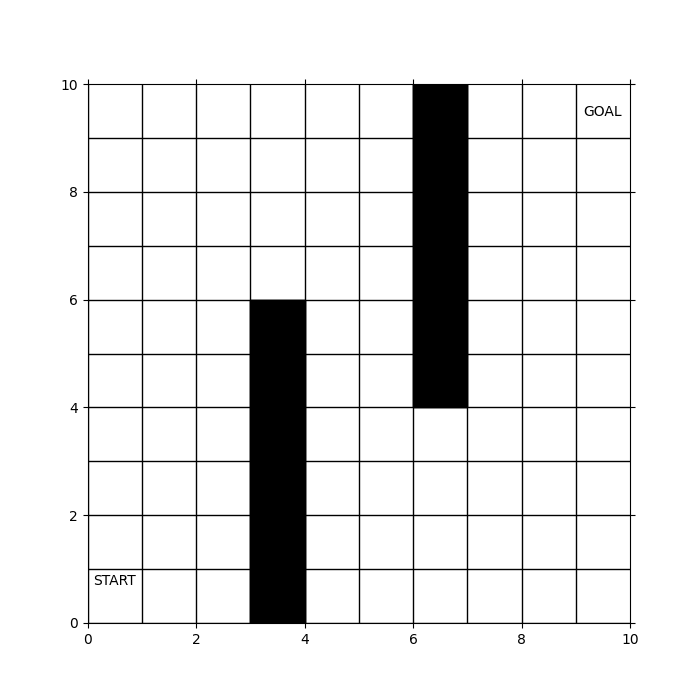
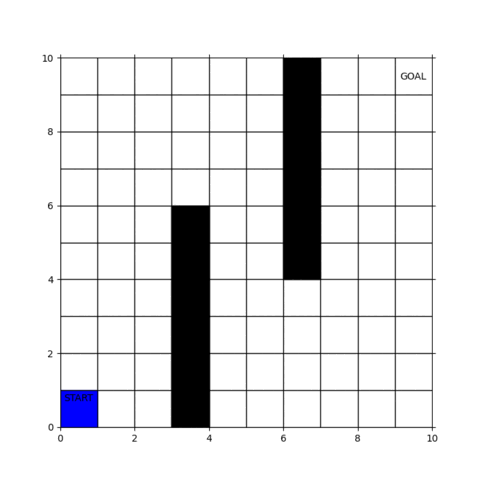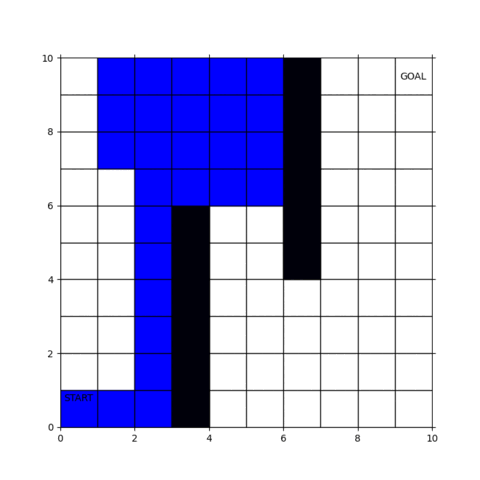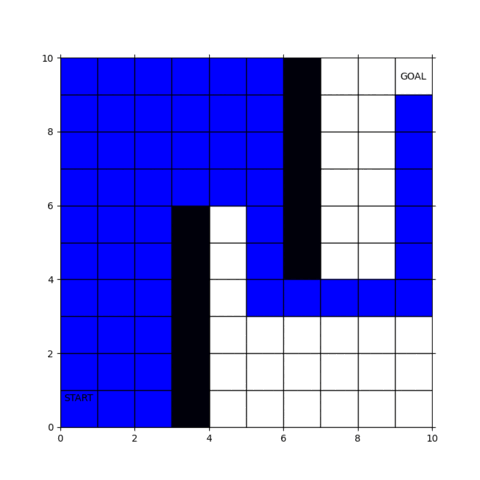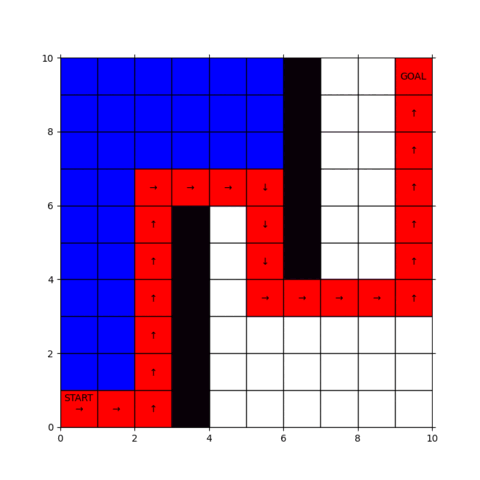
今回のプログラムで使用する地図は10x10の2次元格子地図で、スタート/ゴールがそれぞれ左下/右上に設置し、障害物は黒で表現しています。ロボットは上下左右4方向に移動できるとします。
まず幅優先探索を実行してみましょう。
以下のコマンドを実行します:
$python3 planner.py -p width
実行した結果の動画が下図です。
青い部分が探索範囲で、ゴールに到達すると経路が赤く表示されます。
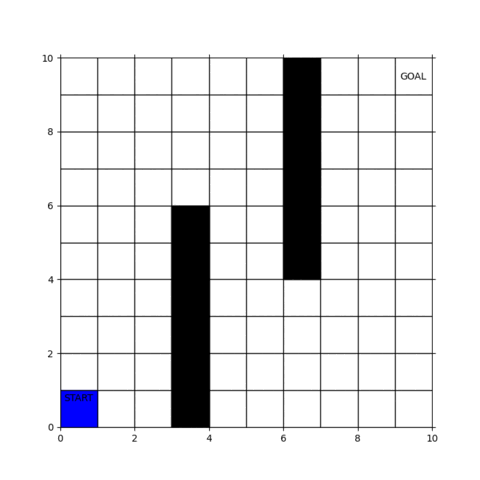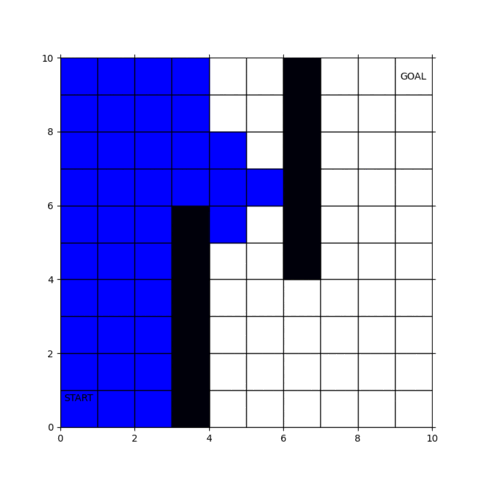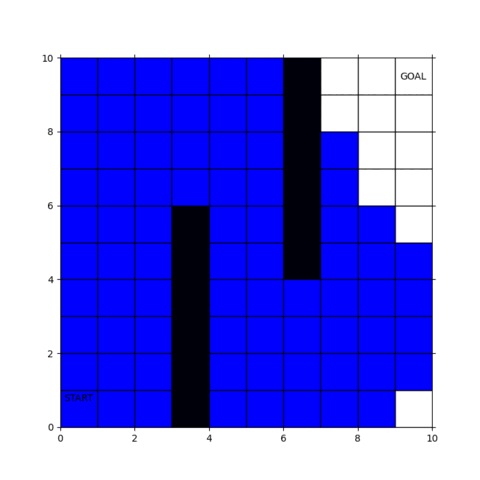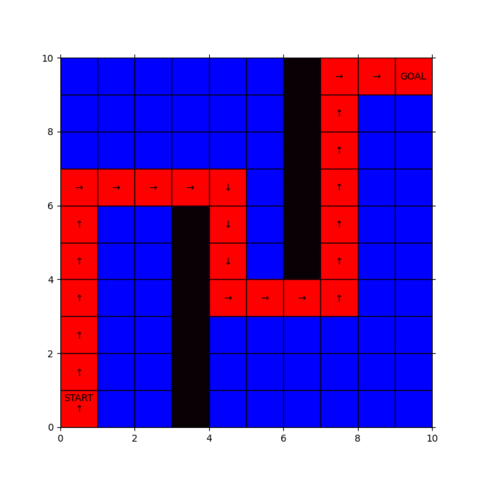
幅優先探索ではスタート地点から近い順にブワッと探索範囲が広がっていくことがわかると思います。
次に、深さ優先探索を実行してみましょう。
以下のコマンドを実行します:
$python3 planner.py -p depth
実行結果の動画が下図です。
「行けるところまで突っ走って、ダメになったら戻り」を繰り返していることが見て取れると思います。
幅優先探索とは全く異なる方針で経路が探索されていることをご確認ください。
なお、GitHubのプログラムは結果のアニメーション表示が可能ですが、動画ファイルとして保存することはできません。
動画を保存するにあたっては下記リンクのスクリプトを用いましたので、保存をしたい方はこちらのリンクを見て適切にコードを変更してください。
幅も深さも「良い」経路計画なのか?
さて、2つの手法を観察すると、どちらも問題なく最も良い経路(障害物を回避しつつ、スタートからゴールまで最短の経路)が計算できているように思えますが、実はこれは間違いです。
冒頭でも少し述べましたが、実は深さ優先探索はゴールの場所が変わると最短経路を計画できなくなります。
実際にゴールを変更して2つのアルゴリズムを動かしてみましょう。
ゴールの場所を変えるには、main関数内のMapperインスタンスの宣言時にゴールの座標を定義している箇所を変更します。
ゴールの座標を[9,9]から[4,0]へ変更してみましょう。
map = Mapper(start=[0,0], goal=[4,0])
幅優先探索の進化版:ダイクストラ法
では幅優先探索なら良いのか、という話ですが、結論から言うと今回の設定では問題ないですが万能ではありません。
今回の設定では「最短=経路全体のマス目の数が少ない」でしたが、下図のようにマス目の「重み」が異なる地図で合った場合「マス目の重みが平等」という暗黙の前提条件があった幅優先探索を利用できません。
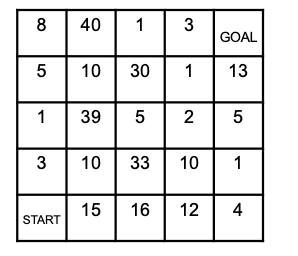
そこで、重みが異なる地図でも最短経路の計算を可能したダイクストラ法が登場します。
ダイクストラ法について解説した記事を作成いたしました。